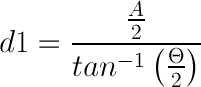人類自古活在天地之間，在地球上大部分地區都可看見太陽東昇西落，天有多高？日有多遠？人類一直嘗試以不同方法估計和測量地球和太陽的距離。古時，世界各地 的人曾經以月相、正午日影、月全食的地影等方法測量，得出不同的地日距離，但往往因為觀測難度、技術或方法限制或錯誤等，這些數字的誤差最大可以與真實相差數千倍。

量度地日距離

直至克普勒在十七世紀提出行星運動定律，人們才比較確切了解行星(包括地球) 的公轉運動。根據克普勒行星運動第三定律：行星公轉周期 (P) 的平方與其太陽平均距離 (a) 的立方成正比。

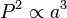
認識行星運動定律，可以得知各行星與太陽之間距離的比例，但要知道真實的距離，則需要測量其中一顆行星與太陽或行星的距離。怎樣可以比較準確量度太陽系內星體的距離？十七到十八世紀的科學家透過觀測罕見的金星凌日，測量地球和金星的距離。

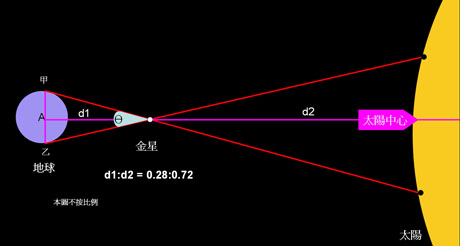
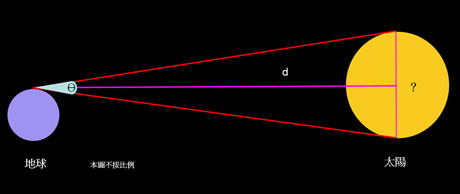
科學家遠道去到地球上相距 A 公里的甲、乙兩地，同時觀測金星凌日。由於兩個地點觀測金星的角度有少許分別，金星的影像則會落在背景上太陽的不同位置。透過量度兩地的觀測位置的角度差Θ，利用三角學的計算，就可以得知地球和金星的距離。這個測量距離的方法，稱為視差法 (parallax) ，亦是人類雙眼可以感覺距離、立體感的原因。

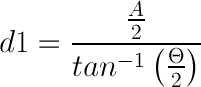
得知 d1 ，就可以利用 d1 和 d2 的比例計算地球和太陽的距離。直至二十世紀中期，才有小行星觀測、無線電波測量等方法，取代金星凌日在測量日地距離的地位。

地日距離的意義

得知地日距離我們可以利用三角學，計算太陽的直徑、體積。

應用行星運動第三定律，可以計算各大行星的距離。

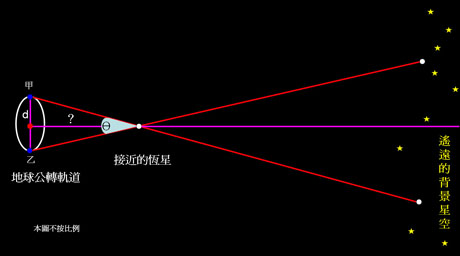
由於太陽系外的星體距離非常遙遠，在地球上的兩點利用視差法不能夠測量較接近地球的恆星極微小的角度差，那麼我們最遠的兩個觀測點在那裡？

在地球公轉的軌道上，甲乙兩點相隔軌道的直徑，即地日距離的兩倍。只要在甲點觀察目標星的相對於背景星空的位置，半年後地球運行至乙點時，再次點觀察目標星就可以計算該星與地球的距離。

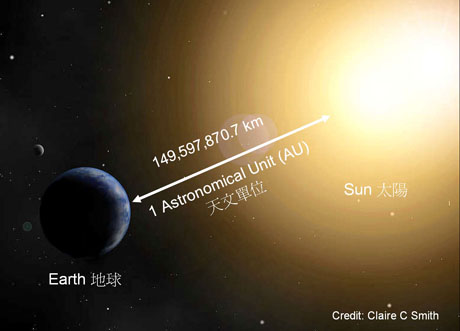
地日距離不單是一個數字，更是人類在太空中第一把尺，打開測量宇宙的大門。所以，為方便表示和計算，地球和太陽的平均距離（約 149,597,871 公里 ） 稱為 1 天文單位 (Astronomical Unit, AU)。

天文導師
曾展鈞